문제 설명
표와 구간을 나타내는 테스트 케이스가 주어질 때, 그 구간까지의 합을 구하는 문제이다.
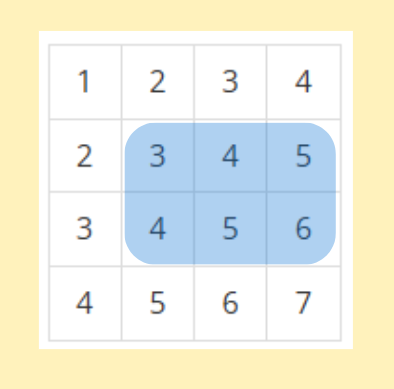
만약 (2,2) - (3,4)의 구간합을 구하는 문제에서는 파란색 칸만큼 더하여 3+4+5+4+5+6 = 27이다.
문제 풀이
구간합으로 풀 수 있었다.
우선 2차원 배열 dp를 선언한다. dp[i][j]는 (0,0) 부터 table[i][j] 까지의 합이다.
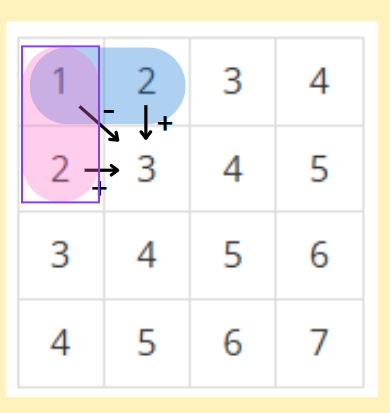
그림에서 보다싶이, 파랑과 빨강이 겹치는 부분이 존재하기 때문에 공통 된 부분은 빼줘야 한다.
코드로 나타내면 다음과 같다.
우선 dp를 (n+1)x(n+1) 사이즈를 0으로 초기화해주고,
1) 왼쪽 dp 값 + 오른쪽 dp 값을 더한다.
2) 대각선 dp 값을 빼준다.
3) 현재 값을 더해준다.
이 과정을 통해 dp에 (0,0) 부터 현재 좌표까지 누적한 값들이 저장되었다.
그렇다면 (s1, s2) ~ (e1, e2) 까지의 합은 어떻게 구할까?

👉 면적 = 파란색 - 빨간색 - 노란색 + 공통된 부분
여기서도 마찬가지로 공통된 부분을 꼭 신경쓰고 더해줘야 한다.
👉 면적 = dp[e1][e2] - dp[e1][s2 - 1] - dp[s1 - 1][e2] + dp[s1 - 1][s2 - 1]
전체 코드
const fs = require("fs");
const input = fs.readFileSync("/dev/stdin", "utf8").trim().split("\n");
const [n, m] = input[0].split(" ").map(Number);
const table = input.slice(1, n + 1).map((line) => line.split(" ").map(Number));
const tc = input.slice(n + 1, n + m + 1).map((line) => line.split(" ").map(Number));
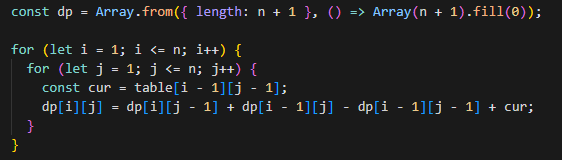
const dp = Array.from({ length: n + 1 }, () => Array(n + 1).fill(0));
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {
const cur = table[i - 1][j - 1];
dp[i][j] = dp[i][j - 1] + dp[i - 1][j] - dp[i - 1][j - 1] + cur;
}
}
for (let i = 0; i < tc.length; i++) {
const [s1, s2, e1, e2] = tc[i];
console.log(dp[e1][e2] - dp[e1][s2 - 1] - dp[s1 - 1][e2] + dp[s1 - 1][s2 - 1]);
}
'Algorithm' 카테고리의 다른 글
| [JavaScript] 12904. A와 B (1) | 2025.03.27 |
|---|---|
| [JavaScript] 1446. 지름길 (1) | 2025.03.26 |
| [Javascript] 백준 1018. 체스판 다시 칠하기 (1) | 2025.03.14 |
| [JavaScript] 백준 1535. 안녕 (1) | 2025.03.12 |
| [JavaScript] 백준 1976 - 여행 가자 (1) | 2025.03.11 |

