
각 도시들 사이에 길이 있을 수도 있고, 없을 수도 있다. 도시들의 연결되어 있는 정보를 보고 여행갈 수 있는 지를 판별하여 "YES"나 "NO"를 출력하면 된다.
도시들이 연결되어있다는 말은 하나의 그래프라는 것이고 유니온 파인드 알고리즘을 사용하여 알 수 있다.
유니온 파인드
각 연결정보가 주어질 때, 그 그래프를 모두 연결해보면 2개의 그래프로 나뉜다는 것을 알 수 있다.
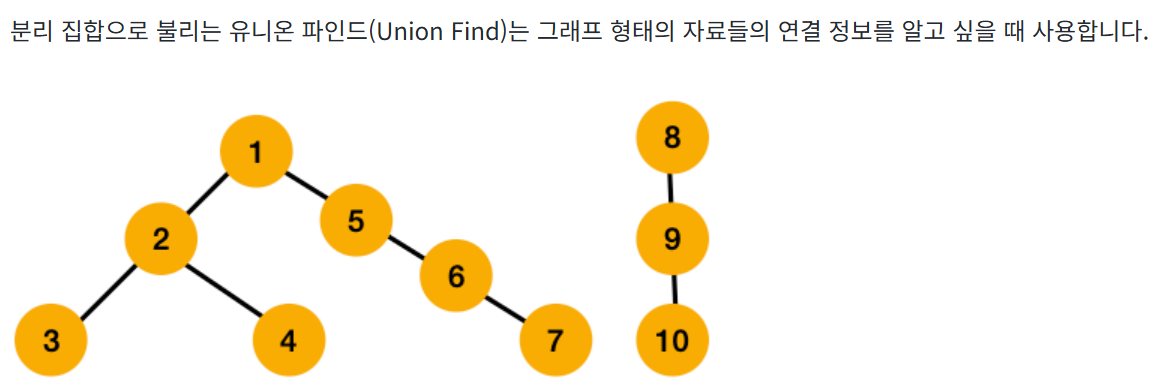
그렇다면 유니온 파인드는 어떻게 구현할까?
유니온 파인드는 부모(Parent) 배열을 사용하여 각 원소가 속한 집합을 나타낸다.
초기에는 각 원소가 자기 자신을 부모로 가지도록 설정한다.
(1) Find 연산 (경로 압축: Path Compression)
Find 연산은 특정 원소가 속한 집합의 대표(root) 원소를 찾는 과정
일반적인 Find 구현은 루트를 찾을 때 단순히 부모 노드를 따라가는 방식이지만, 경로 압축(Path Compression)을 적용하면 Find 연산을 더욱 효율적으로 수행할 수 있습니다.
function find(a) {
if (parents[a] !== a) {
parents[a] = find(parents[a]); // 경로 압축
}
return parents[a];
}경로 압축을 적용하면, Find 호출 이후 같은 집합에 속한 원소들은 루트 노드에 직접 연결된다. 이를 통해 Find 연산의 시간 복잡도를 거의 O(1) 수준으로 줄일 수 있다.
(2) Union 연산
Union 연산은 두 원소가 속한 집합을 하나로 합치는 연산
더 작은 번호의 루트를 우선적으로 부모로 설정
function union(a, b) {
const root1 = find(a);
const root2 = find(b);
if (root1 < root2) {
parents[root2] = root1;
} else {
parents[root1] = root2;
}
}
전체코드
const fs = require("fs");
const input = fs.readFileSync("/dev/stdin", "utf8").trim().split("\n");
const n = Number(input[0]);
const m = Number(input[1]);
const adj = input.slice(2, n + 2).map((line) => line.split(" ").map(Number));
const cities = input[n + 2]
.split(" ")
.map(Number)
.map((city) => city - 1);
const parents = Array.from({ length: n }, (_, i) => i);
adj.forEach((line, from) =>
line.forEach((v, to) => {
if (v === 1) {
union(from, to);
}
})
);
if (cities.length) {
const root = parents[cities[0]];
for (let v of cities) {
if (root != parents[v]) {
console.log("NO");
return;
}
}
}
console.log("YES");
function find(a) {
if (parents[a] !== a) {
parents[a] = find(parents[a]);
}
return parents[a];
}
function union(a, b) {
const root1 = find(a);
const root2 = find(b);
if (root1 < root2) {
parents[root2] = root1;
} else {
parents[root1] = root2;
}
}
문제 링크
https://www.acmicpc.net/problem/1976
참고
'Algorithm' 카테고리의 다른 글
| [Javascript] 백준 1018. 체스판 다시 칠하기 (1) | 2025.03.14 |
|---|---|
| [JavaScript] 백준 1535. 안녕 (1) | 2025.03.12 |
| [JavaScript] 백준 11725 - 트리의 부모 찾기 (0) | 2025.03.05 |
| [Javascript] 프로그래머스 - 서버 증설 횟수 (0) | 2025.02.21 |
| [Javascript] 백준 - Puyo Puyo (0) | 2025.02.20 |


