🧾 목차
1. 설명
2. 알고리즘 접근
3. 문제 풀이
4. 전체 코드
1. 설명
1️⃣ 문제 분석
출발 지점부터 목적 지점(distance) 사이의 돌 들이 있다.
그 돌중에서 n 개의 돌을 삭제하여 각 구간(남은 돌 사이 거리)의 최소 값을 구하고,
이 최소값들 중 가장 큰 값(최대 최소 거리)을 구하는 문제이다.
2️⃣ 입출력
돌의 개수(rocks.length)가 5일 때, 2개의 돌을 삭제하는 경우의 수는,
C(5, 2) = 10
총 10가지의 경우의 수가 존재한다.

해결과정
1) 2개의 돌을 선택하여 제거(총 10가지 조합 가능)
2) 남은 돌들 사이의 거리를 계산
3) 각 경우마다 최소 거리값을 구함
4) 이 최소값들 중 가장 큰 값을 구하면, 4이다.

3️⃣ 제한사항

완전 탐색의 경우, C(바위 개수, 삭제할 바위 수) => 시간 복잡도 초과 예상
2. 알고리즘 접근
바위가 총 50,000개 이기 때문에 그 중 n개를 고르려면, 시간복잡도가 50,000Cn 가 된다.
만약 n = 2 라면, C(50,000, 2) ≃ 1,250,000,000 (시간 복잡도 초과)
따라서, 이분 탐색으로 범위를 줄여야 한다.
📌 이분 탐색을 결정하는 팁
1. 제한 조건이 매우 크다.
2. 배열 정렬이 되어 있어야 한다.
/** 스켈레톤 코드 */
function solution(distance, rocks, n) {
// left, right 지정
var [left, right] = [1, distance]; // 사이 거리의 최소, 사이 거리의 최대
while (left < right) {
// mid 계산
var mid = Math.floor((left + right) / 2);
// 돌 순회하면서 로직 계산
var removed = 0; // 삭제한 돌 개수
for (let i = 0; i < rocks.length; i++) {
...
}
// 범위 조정
if (removed > n) {...}
else {...}
}
}
주어진 문제의 시간 복잡도는 O(MlogN)이고, 제한 사항은 다음과 같다.
- N (거리 distance의 최대값) : 10^9
- M (바위 개수의 최대값) : 50,000
1️⃣ 알고리즘의 흐름을 보면,
- 이진 탐색을 사용하여 가능한 최소 거리의 최대값을 찾음 → O(logN)
- 각 이진 탐색마다 돌을 순회하여 제거할 개수를 체크 → O(M)
따라서, O(MlogN)이다.
2️⃣ 최악의 경우를 고려해봤을 때,
- M = 50,000 (바위 개수 최대값)
- N = 10^9 (거리 최댓값)
따라서, 50,000 x log10^9 = 50,000 x 19log10 = 50,000 x 30 ≃ 1,500,000 번
👉 이진 탐색으로 해결 가능
3. 문제 풀이
이진 탐색의 풀이법은 주로 다음과 같다.
📌 이진 탐색
1. left, right 설정
2. While 문 : 이진 탐색을 사용하여 정답을 찾음
2-1. 중간 값 계산
2-2. For 반복문 : 각 이진 탐색마다 로직을 계산
2-3. left or right를 통해 범위 조정
3. 정답 리턴
1) 초기화
돌 위치를 정렬하고, left, right를 초기화하였다.

2-1) 중간 값 계산
이 때, mid는 돌 사이의 거리중 최소이다.
e.g. [2, 11, 14, 17, 21] / 25(distance) 일 때, 2가 최소

2-2 ) 로직 계산
돌을 순회하며, 돌 사이의 거리가 mid 보다 큰 경우 삭제 카운트 증가
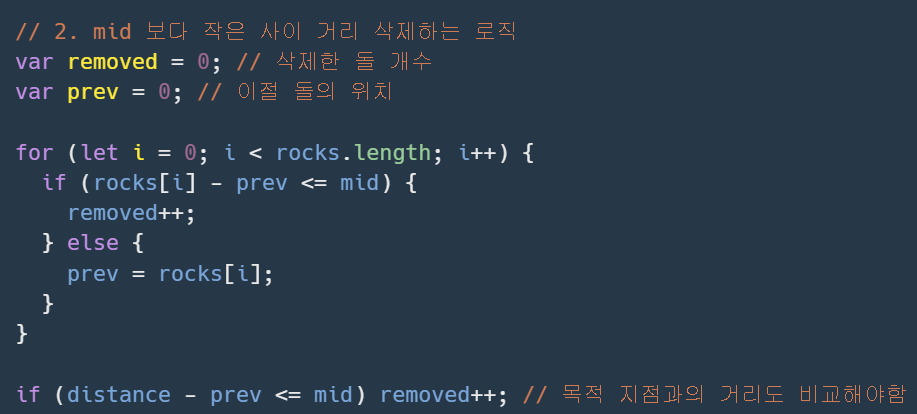
2-3) 범위 조정
removed : 삭제한 돌의 개수, n : 요구된 삭제 바위 수
1️⃣ 너무 많이 삭제한 경우 → 거리를 낮춘다
- removed > n
- 더 많은 바위를 제거했다는 것은, 최소 거리(mid)가 너무 작아서 많은 바위가 제거되었음을 의미함
- 따라서, 최소 거리(mid)를 줄여야 함 → right = mid - 1
2️⃣ 삭제 개수가 요구된 n 이하인 경우 → 거리를 높인다
- removed ≤ n
- 삭제 개수가 n과 같더라도, 더 큰 최소 거리(mid 값)에서 동일한 n개의 바위를 삭제할 수도 있음
- 즉, 더 큰 값을 탐색하여 최소 거리의 최대값을 찾는다 → left = mid + 1

4. 전체 코드
function solution(distance, rocks, n) {
// 돌 위치 정렬
rocks.sort((a, b) => a - b);
var [left, right] = [1, distance]; // 사이 거리의 최소, 사이 거리의 최대
while (left <= right) {
// 1. 중간 값 계산
var mid = Math.floor((left + right) / 2);
// 2. mid 보다 큰 거리 삭제하는 로직
var removed = 0; // 삭제한 돌 개수
var prev = 0; // 이절 돌의 위치
for (let i = 0; i < rocks.length; i++) {
if (rocks[i] - prev <= mid) {
removed++;
} else {
prev = rocks[i];
}
}
if (distance - prev <= mid) removed++; // 목적 지점과의 거리도 비교해야함
// 3. 범위 조정
if (removed > n) {
// 너무 많이 삭제했다면
right = mid - 1;
} else {
// 적게 삭제됐다면
left = mid + 1;
}
}
return left;
}
'Algorithm' 카테고리의 다른 글
| [Javascript] 프로그래머스 - 전력망을 둘로 나누기 (1) | 2025.02.04 |
|---|---|
| [Javascript] 프로그래머스 - 네트워크 (0) | 2025.02.03 |
| [Javascript] 프로그래머스 - 퍼즐 게임 챌린지 (1) | 2025.01.29 |
| [Javascript] 프로그래머스 - 입국심사 (0) | 2025.01.28 |
| [Javascript] 프로그래머스 - 타겟 넘버 (2) | 2025.01.28 |