목차
1. 문제 설명
2. 문제 풀이
3. 전체 코드
1. 문제 설명
모든 음식의 스코빌 지수를 K 이상으로 만드는 데 걸리는 횟수를 구하는 문제이다.
K 이상으로 만들기 위해서, 연산을 해야하는데 그 연산은 다음과 같다.
섞은 음식의 스코빌 지수 = 가장 맵지 않은 음식의 스코빌 지수 + (두 번째로 맵지 않은 음식의 스코빌 지수 * 2)
Key point
제한 조건 : 2 <= scoville의 길이 <= 1,000,000
가장 적은 두 개의 값을 계속 구해야하는데,
그때그때마다 새로운 적은 값을 구하기 위해서는 시간초과가 발생한다.
👉 힙 알고리즘을 구현해내야한다.
2. 문제 풀이
1) 기본 코드
힙을 구현하기 위한 기본 구조는 다음과 같다.
class MinHeap {
constructor() {
this.heap = []; // 힙 배열
}
size() {
return this.heap.length; // 힙의 크기를 반환
}
// 두 인덱스의 값들을 교환하는 메소드
swap(idx1, idx2) {
[this.heap[idx1], this.heap[idx2]] = [this.heap[idx2], this.heap[idx1]];
}
}
2) heappush
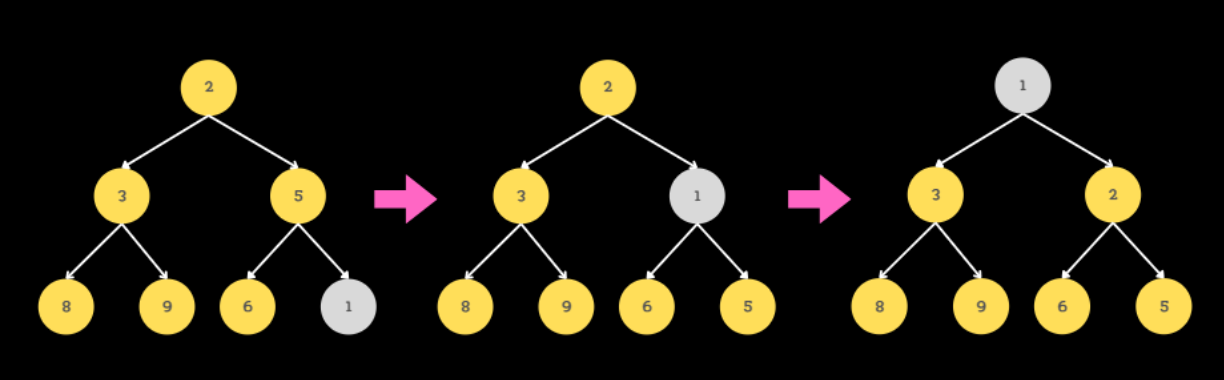
삽입 과정
1) 새로운 노드를 마지막 노드에 추가
2) 부모 노드와 우선순위를 비교하여 높은 것을 위로 올리기(bubble up)
// 힙 삽입 연산하는 함수
heappush(value) {
this.heap.push(value); // 새로운 노드 삽입
this.bubbleUp(); // ⭐ 위치 조정 함수
}
bubbleUp() {
let index = this.size() - 1; // 새로 추가된 노드의 인덱스
let pIndex = Math.floor((index - 1) / 2); // 부모 인덱스
// 부모가 자식보다 크면 교환
while (pIndex >= 0 && this.heap[pIndex] > this.heap[index]) {
this.swap(index, pIndex);
index = pIndex; // 인덱스를 부모로 이동
pIndex = Math.floor((index - 1) / 2); // 새로운 부모 인덱스
}
}
3) heappop
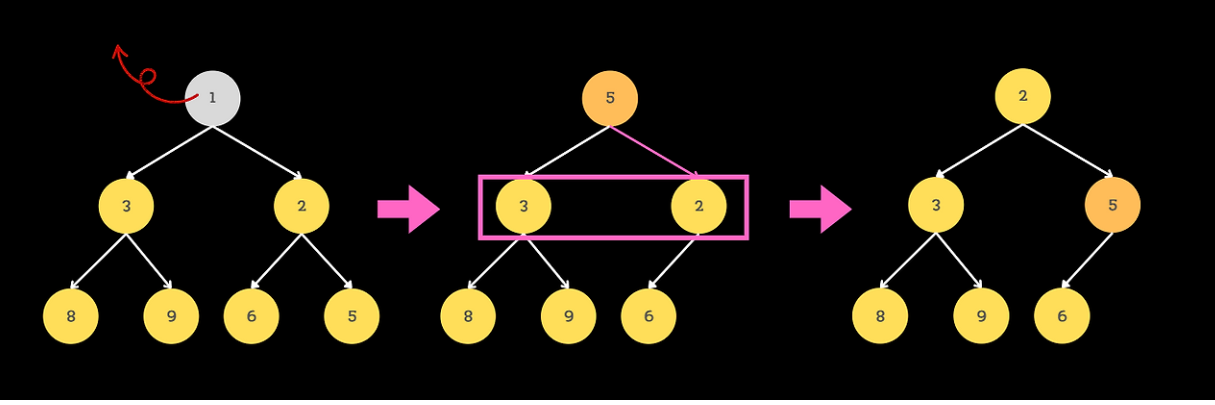
삭제 과정
1) 루트 노드를 제거
2) 마지막 노드의 값을 루트 노드로 이동
3) 루트 노드부터 자식 노드와 비교하여 자식 노드가 우선순위가 더 높으면 아래로 내리기(bubble down)
- 이 때 두 개의 자식 노드 중 우선 순위가 더 높은 자식 노드와 부모를 비교해아함
// 힙 삭제 연산하는 함수
heappop() {
// 루트노드만 있는 경우
if (this.size() === 1) {
return this.heap.pop();
}
const value = this.heap[0]; // 루트 노드의 값을 저장
this.heap[0] = this.heap.pop(); // 마지막 노드의 값을 루트로 이동
this.bubbleDown(); // ⭐ 위치 조정
return value; // 루트 노드의 값 반환( = 가장 적은 값)
}
bubbleDown() {
let index = 0; // 루트 노드의 인덱스
let leftIndex = index * 2 + 1; // 왼쪽 자식의 인덱스
let rightIndex = index * 2 + 2; // 오른쪽 자식의 인덱스
// 부모가 자식보다 크면 반복
while (
(this.heap[leftIndex] && this.heap[leftIndex] < this.heap[index]) ||
(this.heap[rightIndex] && this.heap[rightIndex] < this.heap[index])
) {
let smallerIndex = leftIndex; // 두 개의 자식 중 더 작은 노드의 인덱스
if (
this.heap[rightIndex] &&
this.heap[rightIndex] < this.heap[smallerIndex]
) {
smallerIndex = rightIndex;
}
this.swap(index, smallerIndex); // 값 교환
index = smallerIndex; // 인덱스를 자식으로 이동
leftIndex = index * 2 + 1; // 자식 노드의 인덱스를 재계산
rightIndex = index * 2 + 2; // 오른쪽 노드의 인덱스를 재계산
}
}
3. 정답 코드
class MinHeap {
constructor() {
this.heap = [];
}
size() {
return this.heap.length;
}
swap(idx1, idx2) {
[this.heap[idx1], this.heap[idx2]] = [this.heap[idx2], this.heap[idx1]];
}
heappush(value) {
this.heap.push(value);
this.bubbleUp();
}
bubbleUp() {
let index = this.size() - 1;
let pIndex = Math.floor((index - 1) / 2);
while (pIndex >= 0 && this.heap[pIndex] > this.heap[index]) {
this.swap(index, pIndex);
index = pIndex;
pIndex = Math.floor((index - 1) / 2);
}
}
heappop() {
if (this.size() === 1) {
return this.heap.pop();
}
const value = this.heap[0];
this.heap[0] = this.heap.pop();
this.bubbleDown();
return value;
}
bubbleDown() {
let index = 0;
let leftIndex = index * 2 + 1;
let rightIndex = index * 2 + 2;
while (
(this.heap[leftIndex] && this.heap[leftIndex] < this.heap[index]) ||
(this.heap[rightIndex] && this.heap[rightIndex] < this.heap[index])
) {
let smallerIndex = leftIndex;
if (this.heap[rightIndex] && this.heap[rightIndex] < this.heap[smallerIndex]) {
smallerIndex = rightIndex;
}
this.swap(index, smallerIndex);
index = smallerIndex;
leftIndex = index * 2 + 1;
rightIndex = index * 2 + 2;
}
}
}
function solution(scoville, K) {
let answer = 0;
const heap = new MinHeap();
scoville.forEach((v) => heap.heappush(v));
while (heap.size() >= 2) {
let a = heap.heappop();
let b = heap.heappop();
if (a >= K) {
return answer;
}
let newOne = a + b * 2;
heap.heappush(newOne);
answer +=1;
}
return heap.size() > 0 && heap.heappop() >= K ? answer : -1;
}
'Algorithm' 카테고리의 다른 글
| [Javascript] 프로그래머스 - 모음 사전 (0) | 2025.01.22 |
|---|---|
| [Javascript] 소수 찾기 (1) | 2025.01.21 |
| [Javascript] 가장 큰 수 (0) | 2025.01.11 |
| [Javascript] 롤케이크 자르기 (0) | 2025.01.11 |
| 순열, 조합 문제 풀이 (with. Python) (3) | 2024.12.13 |



