목차
1. 문제 접근
2. 문제 풀이
3. 정답 코드
1. 문제 접근
삼각형의 맨 꼭대기에서 바닥까지 내려가면서, 거쳐한 수들의 합이 최댓값이 되는 수를 리턴한다.
아래칸으로 이동할 때는 왼쪽 대각선, 오른쪽 대각선 아래로 이동한다.
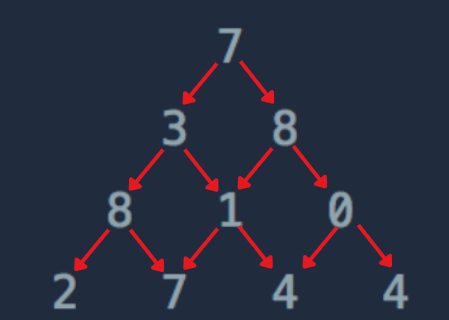
화살표 방향으로 이동하면서 그 수들을 계속 더해주면 되기 때문에, 누적합 문제이다.
누적합이란, a[i] = a[i-1] + ??
이런식으로 구현하는 것을 말한다.
그렇다면 2차원 배열로 주어지는 triangle 배열에서는 어떤식으로 누적합을 해줘야 할까?
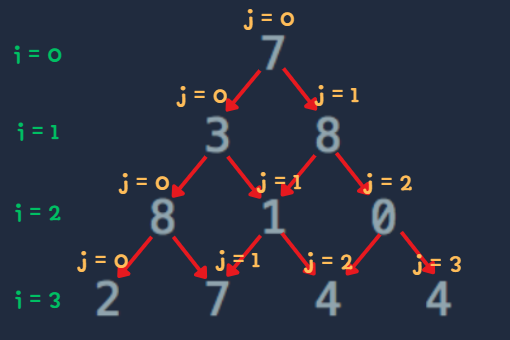
i = 2일 경우를 살펴보자
✔ j = 0 또는 j == i 일 때를 제외하고, 즉 맨 앞과 맨 뒤를 제외하고는 기본적으로 화살표가 양쪽에서 오는 것을 확인할 수 있다.
그 화살표들 중 최댓값을 누적해서 더해주면 된다.
triangle[i][j] += Math.max(triangle[i-1][j-1], triangle[i-1][j]);
✔ 맨 앞일 때는 triangle[i-1][0] 에서만 화살표가 나온다.
triangle[i][0] += triangle[i-1][0];
✔ 맨 뒤일 때는 triangle[i-1][j-1] 에서만 화살표가 나온다.
triangle[i][j] += triangle[i-1][j-1];2. 문제 풀이
각 위치로 오는 화살표를 고려하여 값을 누적하는 방법은 다음 세 가지 경우로 나눌 수 있다.
i) 맨 앞(j = 0) 일 때
- 왼쪽에서만 값이 전달되므로, 바로 위(triangle[i-1][0])의 값만 더해주면 된다.
ii) 맨 끝(j == i) 일 때
- 오른쪽 위(triangle[i-1][j-1])에서만 값이 전달된다.
iii ) 그 외의 경우
- 왼쪽 위(triangle[i-1][j-1])와 오른쪽 위(triangle[i-1][j])에서 두 개의 값이 들어온다.
- 두 값 중 최댓값을 선택해 현재 값에 더해준다.
이를 코드로 나타내면 다음과 같다.
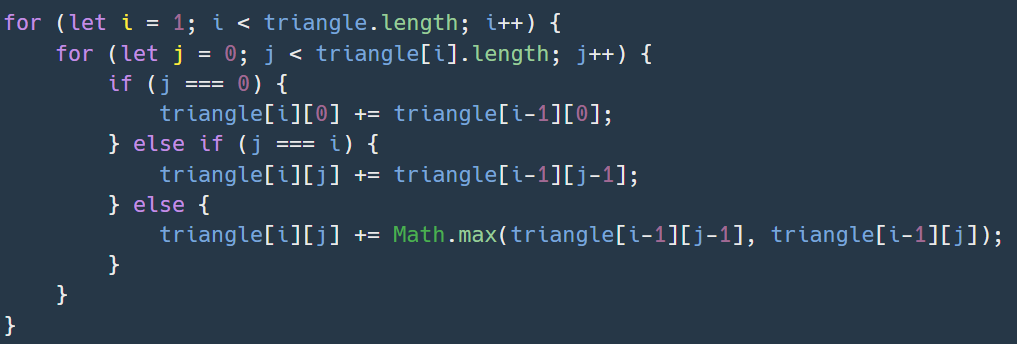
3. 정답 코드
function solution(triangle) {
var answer = 0;
for (let i = 1; i < triangle.length; i++) {
for (let j = 0; j < triangle[i].length; j++) {
if (j === 0) {
triangle[i][0] += triangle[i-1][0];
} else if (j === i) {
triangle[i][j] += triangle[i-1][j-1];
} else {
triangle[i][j] += Math.max(triangle[i-1][j-1], triangle[i-1][j]);
}
}
}
return Math.max(...triangle[triangle.length -1]);
}'Algorithm' 카테고리의 다른 글
| [Javascript] 백준 - Puyo Puyo (0) | 2025.02.20 |
|---|---|
| [Javascript] 백준 - 외판원 순회 2 (0) | 2025.02.17 |
| [Javascript] 가장 먼 노드 (0) | 2025.02.13 |
| [Javascript] 프로그래머스 - 게임 맵 최단거리 (2) | 2025.02.05 |
| [Javascript] 프로그래머스 - 아이템 줍기 (0) | 2025.02.05 |



